Gonka算法系列第二篇：深入算法核心之PoW 2.0的统计可重现性实现

引言：从系统架构到可重现性保证

在传统区块链系统中，工作量证明主要依靠哈希运算的随机性来保证安全性。而Gonka PoW 2.0面临着更复杂的挑战：如何在基于大语言模型的计算任务中，既保证计算结果的不可预测性，又确保任何诚实节点都能重现和验证相同的计算过程。本文将深入分析MLNode端如何通过精心设计的种子机制和确定性算法来实现这一目标。

在深入了解具体的技术实现之前，我们需要先理解PoW 2.0系统架构的整体设计，以及可重现性在其中扮演的关键角色。

1. PoW 2.0系统架构概览

1.1 分层架构设计

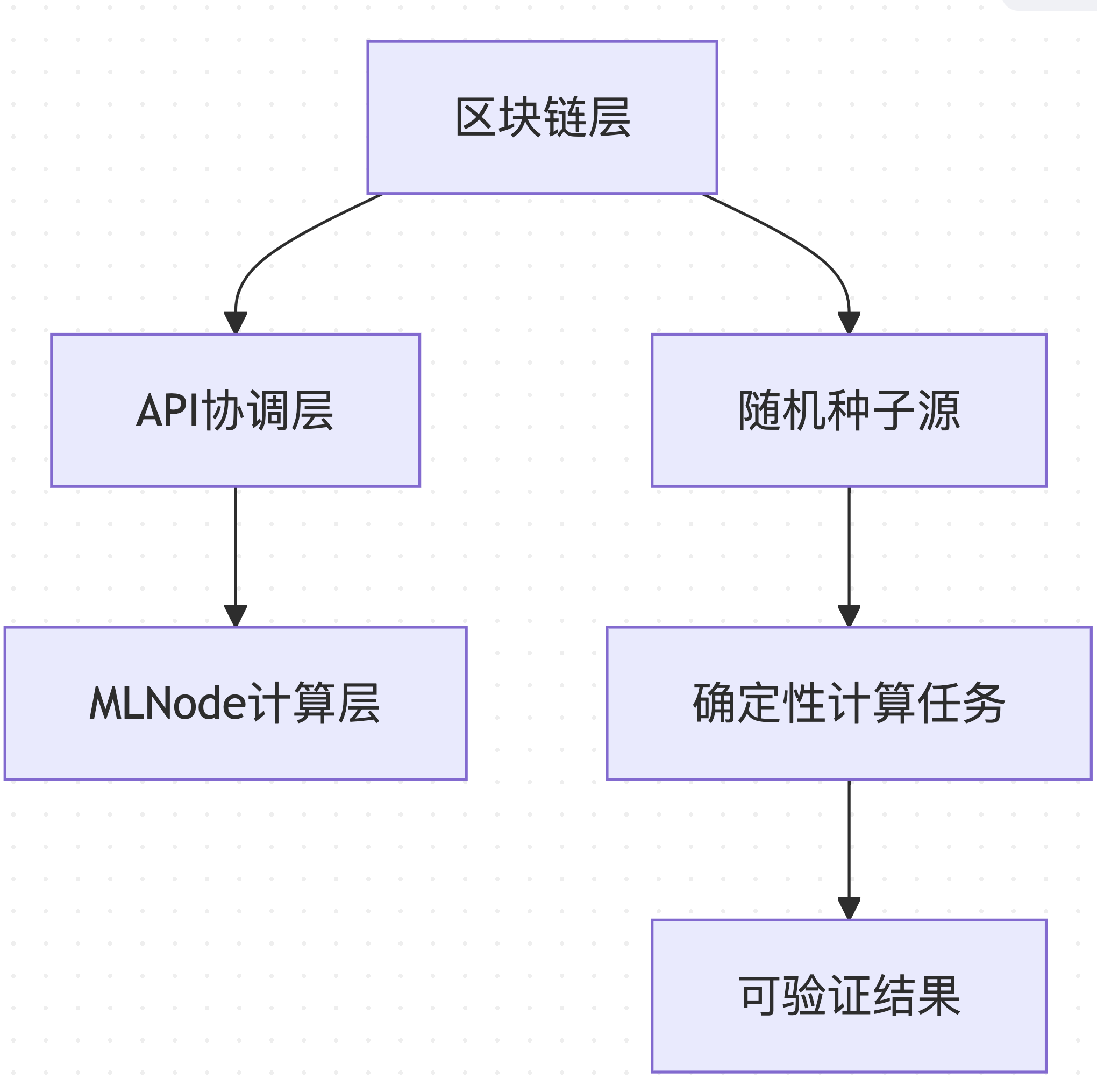
Gonka PoW 2.0采用分层架构，确保可重现性从区块链层面贯穿到计算执行层面：

数据来源 ：基于 decentralized-api/internal/poc 和 mlnode/packages/pow 的架构设计

这种分层设计使得系统的不同组件可以独立优化，同时保持整体的一致性和可验证性。

1.2 可重现性的核心目标

PoW 2.0系统的可重现性设计服务于以下核心目标：

1. 计算公平性 ：确保所有节点面临相同的计算挑战

2. 结果验证性 ：任何诚实节点都能重现和验证计算结果

3. 防作弊保证 ：使预计算和结果伪造在计算上不可行

4. 网络同步 ：确保分布式环境下的状态一致性

这些目标共同构成了PoW 2.0可重现性设计的基础，确保了系统的安全性和公平性。

2. 种子系统：多层次随机性的统一管理

在了解了系统架构之后，我们需要深入探讨实现可重现性的关键技术——种子系统。这个系统通过多层次的随机性管理，确保了计算的一致性和不可预测性。

2.1 种子类型与特定目标

Gonka PoW 2.0设计了四种不同类型的种子，每种服务于特定的计算目标：

网络级种子（Network-Level Seeds）

数据来源 ：decentralized-api/internal/poc/random_seed.go#L90-L111

目标 ：为整个网络的每个epoch提供统一的随机性基础，确保所有节点使用相同的全局随机源。

网络级种子是整个系统随机性的根基，通过区块链交易确保全网节点使用相同的随机性基础。

任务级种子（Task-Level Seeds）

数据来源 ：mlnode/packages/pow/src/pow/random.py#L9-L21

目标 ：通过多轮SHA-256哈希扩展熵空间，为每个计算任务生成高质量的随机数生成器。

任务级种子通过扩展熵空间，为每个具体的计算任务提供高质量的随机性。

节点级种子（Node-Level Seeds）

数据来源 ：种子字符串构造模式 `f"{hash_str}_{public_key}_nonce{nonce}"`

目标 ：确保不同节点和不同nonce值产生完全不同的计算路径，防止碰撞和重复。

节点级种子通过结合节点公钥和nonce值，确保每个节点的计算路径都是唯一的。

目标向量种子（Target Vector Seeds）

数据来源 ：mlnode/packages/pow/src/pow/random.py#L165-L177

目标 ：为整个网络生成统一的目标向量，所有节点都朝着相同的高维球面位置进行优化。

目标向量种子确保全网节点朝着相同的目标进行计算，这是验证结果一致性的关键。

2.2 种子生命周期管理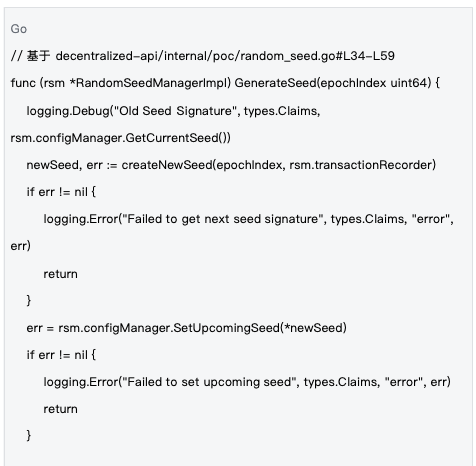

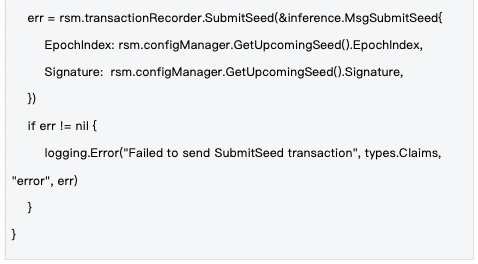
管理机制 ：种子在epoch级别进行管理，每个epoch开始时生成新种子，通过区块链交易同步到全网，确保所有节点使用相同的随机性基础。

种子的生命周期管理确保了随机性的时效性和一致性，是系统安全运行的重要保障。

3. LLM组件的种子驱动生成机制

在了解了种子系统之后，我们需要进一步探讨如何将这些种子应用到LLM组件的生成过程中。这是实现可重现性的关键环节。

3.1 模型权重的随机初始化

为什么需要随机初始化模型权重？

在传统的深度学习中，模型权重通常通过预训练获得。但在PoW 2.0中，为了确保：

1. 计算任务的不可预测性 ：相同的输入不会因为固定权重而产生可预测的输出

2. ASIC抗性 ：专用硬件无法针对固定权重进行优化

3. 公平竞争 ：所有节点使用相同的随机初始化规则

数据来源 ：mlnode/packages/pow/src/pow/random.py#L71-L88

随机初始化模型权重是确保计算不可预测性和公平性的关键步骤。

权重初始化的确定性过程

数据来源 ：mlnode/packages/pow/src/pow/compute/model_init.py#L120-L125

关键特性 ：

• 使用区块哈希作为随机种子，确保所有节点生成相同的权重

• 采用正态分布 N(0, 0.02²) 进行权重初始化

• 支持不同的数据类型（如float16）进行内存优化

这种确定性过程确保了不同节点在相同条件下生成完全一致的模型权重。

3.2 输入向量生成机制

为什么需要随机输入向量？

传统PoW使用固定的数据（如交易列表）作为输入，但PoW 2.0需要为每个nonce生成不同的输入向量，确保：

1. 搜索空间的连续性 ：不同nonce对应不同的计算路径

2. 结果的不可预测性 ：输入的微小变化导致输出的巨大差异

3. 验证的高效性 ：验证者可以快速重现相同的输入

数据来源 ：mlnode/packages/pow/src/pow/random.py#L129-L155

随机输入向量的生成确保了计算的多样性和不可预测性。

输入生成的数学基础

数据来源 ：mlnode/packages/pow/src/pow/random.py#L28-L40

技术特点 ：

• 每个nonce对应唯一的种子字符串

• 使用标准正态分布生成嵌入向量

• 支持批量生成以提高效率

这种数学基础确保了输入向量的质量和一致性。

3.3 输出排列（Permutations）生成

为什么需要输出排列？

在LLM的输出层，词汇表通常很大（如32K-100K个token）。为了增加计算复杂度和防止针对性优化，系统对输出向量进行随机排列：

数据来源 ：mlnode/packages/pow/src/pow/random.py#L158-L167

输出排列增加了计算的复杂度，提高了系统的安全性。

排列的应用机制

数据来源 ：基于 mlnode/packages/pow/src/pow/compute/compute.py 中的处理逻辑

设计目标 ：

• 增加计算挑战的复杂度

• 防止对特定词汇表位置的优化

• 保持确定性以支持验证

这种应用机制确保了排列的有效性和一致性。

4. 目标向量与球面距离计算

在了解了LLM组件的生成机制之后，我们需要进一步探讨PoW 2.0中核心的计算挑战——目标向量与球面距离计算。

4.1 什么是目标向量？

目标向量是PoW 2.0计算挑战的"靶心"——所有节点都尝试让自己的模型输出尽可能接近这个预定的高维向量。

目标向量的数学性质

数据来源 ：mlnode/packages/pow/src/pow/random.py#L43-L56

关键特性 ：

• 向量位于高维单位球面上（||target|| = 1）

• 使用Marsaglia方法确保球面均匀分布

• 所有维度具有相等的被选中概率

目标向量的数学性质确保了计算挑战的公平性和一致性。

4.2 为什么在球面上比较结果？

数学优势

1. 归一化优势 ：球面上的所有向量都具有单位长度，消除了向量幅度的影响

2. 几何直观性 ：欧氏距离在球面上直接对应角度距离

3. 数值稳定性 ：避免了大数值范围带来的计算不稳定

高维几何的特殊性质

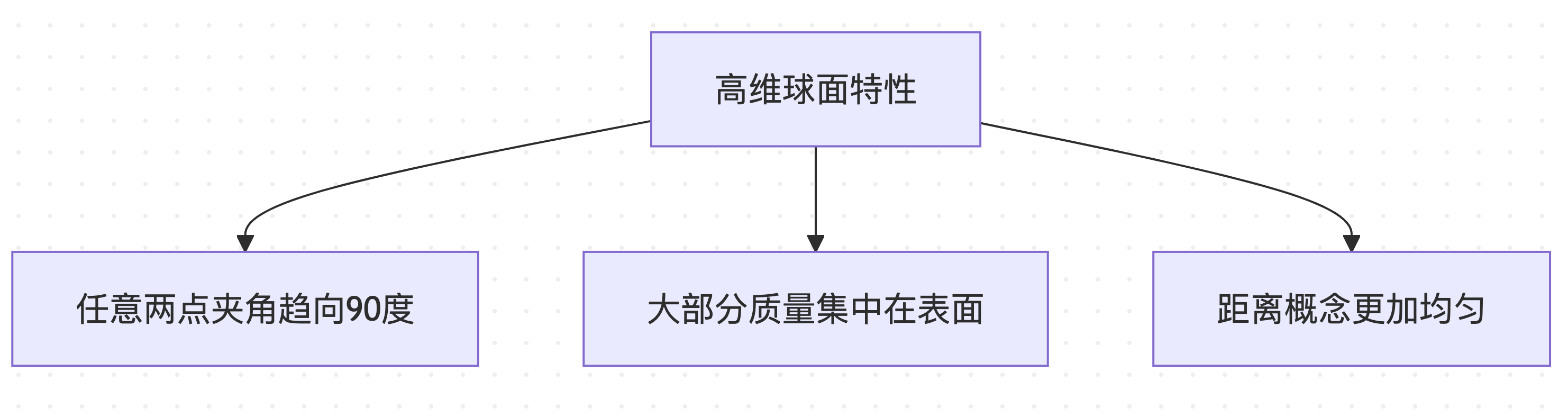
在高维空间（如4096维的词汇表空间）中，球面分布具有反直觉的特性：

这些特殊性质使得球面距离计算成为理想的计算挑战度量。

4.3 r_target估计与PoC阶段初始化

r_target的概念与计算

r_target 是一个关键的难度参数，定义了"成功"计算结果的距离阈值。距离小于 r_target 的结果被认为是有效的工作量证明。

数据来源 ：decentralized-api/mlnodeclient/poc.go#L12-L14

在Gonka PoW 2.0中，r_target 的默认值被设置为 1.4013564660458173，这个值是通过大量实验和统计分析确定的，旨在平衡计算难度和网络效率。虽然系统中有动态调整机制，但大多数情况下都会接近这个默认值。

PoC阶段的r_target初始化

在每个PoC（Proof of Computation）阶段开始时，系统需要：

1. 评估网络算力 ：基于历史数据估算当前网络的总计算能力

2. 调整难度参数 ：设置合适的 `r_target` 值以维持稳定的出块时间

3. 同步全网参数 ：确保所有节点使用相同的 `r_target` 值

技术实现 ：

• r_target 值通过区块链状态同步到所有节点

• 每个PoC阶段可能使用不同的 r_target 值

• 自适应调整算法根据前一阶段的成功率调整难度

这种初始化机制确保了网络的稳定运行和公平性。

5. 可重现性的工程保证

在了解了核心算法之后，我们需要关注如何在工程实现上保证可重现性。这是确保系统在实际部署中稳定运行的关键。

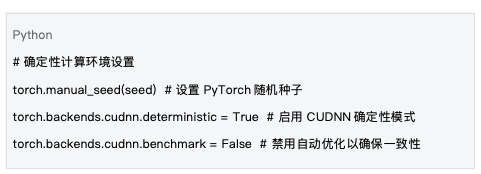
5.1 确定性计算环境

数据来源 ：基于 mlnode/packages/pow/src/pow/compute/model_init.py 的环境设置

确定性计算环境的设置是保证可重现性的基础。

5.2 数值精度管理

数值精度管理确保了在不同硬件平台上计算结果的一致性。

5.3 跨平台兼容性

系统设计考虑了不同硬件平台的兼容性：

- CPU vs GPU ：支持在CPU和GPU上产生相同的计算结果

- 不同GPU型号 ：通过标准化的数值精度确保一致性

- 操作系统差异 ：使用标准的数学库和算法

跨平台兼容性确保了系统在各种部署环境中的稳定运行。

6. 系统性能与可扩展性

在保证可重现性的基础上，系统还需要具备良好的性能和可扩展性。这是确保网络高效运行的关键。

6.1 并行化策略

数据来源 ：mlnode/packages/pow/src/pow/compute/model_init.py#L26-L53

并行化策略充分利用了现代硬件的计算能力。

6.2 内存优化

系统通过多种策略优化内存使用：

- 批处理优化 ：自动调整批处理大小以最大化GPU利用率

- 精度选择 ：使用float16减少内存占用

- 梯度管理 ：在推理模式下禁用梯度计算

内存优化确保了系统在资源受限环境中的高效运行。

总结：可重现性设计的工程价值

在深入分析了PoW 2.0的可重现性设计之后，我们可以总结其技术成就和工程价值。

核心技术成就

1. 多层次种子管理 ：从网络级到任务级的完整种子体系，确保计算的确定性和不可预测性的平衡

2. LLM组件的系统化随机化 ：模型权重、输入向量、输出排列的统一随机化框架

3. 高维几何的工程应用 ：利用球面几何特性设计公平的计算挑战

4. 跨平台可重现性 ：通过标准化算法和精度控制确保不同硬件平台的一致性

这些技术成就共同构成了PoW 2.0可重现性设计的核心。

系统设计的创新价值

Gonka PoW 2.0在保持区块链安全性的同时，成功地将计算资源从无意义的哈希运算转向有价值的AI计算。其可重现性设计不仅确保了系统的公平性和安全性，更为未来的"有意义挖矿"模式提供了可行的技术范式。

技术影响 ：

• 为分布式AI计算提供了可验证的执行框架

• 证明了复杂AI任务与区块链共识的兼容性

• 建立了新型工作量证明的设计标准

通过精心设计的种子系统和确定性算法，Gonka PoW 2.0实现了从传统"浪费型安全"到"价值型安全"的根本转变，为区块链技术的可持续发展开辟了新的道路。

注：本文基于Gonka项目的实际代码实现编写，所有代码示例和技术描述均来自项目官方代码库。

关于 Gonka.ai

Gonka 是一个旨在提供高效 AI 算力的去中心化网络，其设计目标是最大限度地利用全球 GPU 算力，完成有意义的 AI 工作负载。通过消除中心化守门人，Gonka 为开发者和研究人员提供了无需许可的算力资源访问，同时通过其原生代币 GNK 奖励所有参与者。

Gonka 由美国 AI 开发商 Product Science Inc. 孵化。该公司由 Web 2 行业资深人士、前 Snap Inc. 核心产品总监 Libermans 兄妹创立，并于 2023 年成功融资 1800 万美元，投资者包括 OpenAI 投资方 Coatue Management、Solana 投资方 Slow Ventures、K 5、Insight and Benchmark 合伙人等。项目的早期贡献者包括 6 blocks、Hard Yaka、Gcore 和 Bitfury 等 Web 2-Web 3 领域的知名领军企业。

官网 | Github | X | Discord | 白皮书 | 经济模型 | 用户手册