刚出炉的V神论文接好了！STARKs III：攻坚（上）

以太坊创始人Vitalik Buterin 7月21日在其个人网站上发布了论文 STARKs III: Into the Weeds。 此论文为其系列文章的第三篇。

以下为其中文译文：

特别感谢Eli ben Sasson一如既往地提供帮助；也特别感谢Chih-Cheng Liang和Justin Drake的审阅。

前方高能：以下内容涉及大量数学与python

为本系列的第1部分[1]和第2部分[2]的后续内容，本文将介绍在实际中实现STARK的途径与效果，并使用python语言进行实现。STARKs（“可扩展的透明知识参数”是一种用于构建关于f(x)=y 的证明的技术。其中，f 可能需要很长时间来计算，但该证明可以非常快速地得到验证。STARK是“双重可扩展的”：对于带有 t 步的计算，其需要大约O(t * log(t))步来生成证明，这可能是最优的；并且其需要 ~O(log2(t))步来进行验证。在这种方式中，哪怕 t 的值很大，只要在一定范围内，那么计算过程也比原始计算要快得多。STARK同样拥有可进行隐私保护“零知识”属性。尽管我们将这一属性应用到本用例中，但是创建可验证的延迟函数并不需要这个属性，所以我们不需要担心。

首先，以下是关于本文的免责声明：

现在，我们进入正题。

MIMC

这是我们将要实现的STARK函数：

def mimc(inp, steps, round_constants):

start_time = time.time()

for i in range(steps-1):

inp = (inp**3 + round_constants[i % len(round_constants)]) % modulus

print(“MIMC computed in %.4f sec” % (time.time() – start_time))

return inp

我们之所以选择MIMC（参见论文[5]）作为例子，是因为它既（i）易于理解，同时（ii）足够有趣，并且在现实生活中实在的用处。该函数可被看作下图的形式：

注意：在许多关于MIMC的讨论中，你通常会看到人们使用的是XOR而不是+。这是因为MIMC通常在二进制域上完成，而二进制域的加法就是XOR。在这里，我们主要围绕素域进行。

在本例中，循环常量是一个相对较小的列表（例如只包含64项），列表中的数据不断循环（也就是说，在k[64]之后循环回到k[1]）。

正如我们在这里所做的那样，具有非常多轮次的MIMC作为可验证的延迟函数是非常有用的——这是一种难以计算的函数，尤其是无法并行计算，但验证过程相对容易。MIMC本身在某种程度上实现了“零知识”属性，因为MIMC可以“向后”计算（从其相应的“输出”中恢复“输入”），但向后计算需要的计算时间比向前计算多100倍（并且两种方向的计算时间都无法通过并行化来显著加快）。因此，你可以将向后计算函数视为“计算”不可并行化工作量证明的行为，并将前向计算函数计算为“验证”它的过程。

我们可以由x -> x^(2p-1)/3 得出x -> x^3的倒数。根据费马的小定理[6]，这是正确的。费马小定理尽管“小”，但毫无疑问，它对数学的重要性要大于更着名的“费马最后定理”。

我们在这里尝试实现的是，通过使用STARK使验证更有效——相对于验证者必须自己在前向运行MIMC，证明者在完成“后向”计算后，将计算“前向”计算的STARK，并且验证者只需简单地验证STARK。我们希望计算STARK的开销能够小于前向运行MIMC的速相对于后向的速度差异，因此证明者的时间仍将由最初的“后向”计算而不是（高度可并行化的）STARK计算主导。无论原始计算的耗时多长，STARK的验证都可以相对较快（在我们的python实现中，约为0.05到0.3秒）。

所有计算均以2^256 – 351 * 2^32 + 1为模。我们之所以使用这个素域模数是因为它是2^256以内最大的素数，它的乘法组包含一个2^32阶亚组（也就是说，存在数字g，使得g的连续幂模这个素数之后能够在2^32个循环以后回到1） ，其形式为6k + 5。第一个属性是必要的，它确保我们的FFT和FRI算法的有效版本可以发挥作用。第二个属性确保MIMC实际上可以“向后”计算（参见上述关于x -> x^(2p-1)/3的使用）。

素域运算

我们首先构建一个可进行素域运算以及在素域上进行多项式运算的方便的类。其代码在此[7]。初始的细节如下：

class PrimeField():

def __init__(self, modulus):

# 快速素性检验

assert pow(2, modulus, modulus) == 2

self.modulus = modulus

def add(self, x, y):

return (x+y) % self.modulus

def sub(self, x, y):

return (x-y) % self.modulus

def mul(self, x, y):

return (x*y) % self.modulus

以及用于计算模逆的扩展欧几里德算法[8]（相当于在素域中计算1 / x）：

＃使用扩展的欧几里德算法进行模逆计算

def inv(self, a):

if a == 0:

return 0

lm, hm = 1, 0

low, high = a % self.modulus, self.modulus

while low > 1:

r = high//low

nm, new = hm-lm*r, high-low*r

lm, low, hm, high = nm, new, lm, low

return lm % self.modulus

上述算法的开销相对较大。所幸的是，在需要进行众多模逆计算的特殊情况中，有一个简单的数学技巧可以帮助我们计算多个逆，我们称之为蒙哥马利批量求逆[9]：

使用蒙哥马利批量求逆来计算模逆，其输入为紫色，输出为绿色，乘法门为黑色，红色方块是_唯一的_模逆。

下述代码实现了这个算法，并附有一些略微丑陋的特殊情况逻辑。如果我们正在求逆的集合中包含零，那么它会将这些零的逆设置为0并继续前进。

def multi_inv(self, values):

partials = [1]

for i in range(len(values)):

partials.append(self.mul(partials[-1], values[i] or 1))

inv = self.inv(partials[-1])

outputs = [0] * len(values)

for i in range(len(values), 0, -1):

outputs[i-1] = self.mul(partials[i-1], inv) if values[i-1] else 0

inv = self.mul(inv, values[i-1] or 1)

return outputs

当我们开始处理多项式的求值集合划分时，这种批量求逆算法将会非常重要。

现在我们继续进行多项式运算。我们将多项式视为一个数组，其中元素 i 是第 i 次项（例如， x^3 + 2x + 1变为[1,2,0,1]）。以下是对某一点上的多项式求值的运算：

＃对某一点上的多项式求值

def eval_poly_at(self, p, x):

y = 0

power_of_x = 1

for i, p_coeff in enumerate(p):

y += power_of_x * p_coeff

power_of_x = (power_of_x * x) % self.modulus

return y % self.modulus

思考题：

如果模数为31，那么f.eval_poly_at([4, 5, 6], 2) 的输出是多少？

答案是：

6 * 2^2 + 5 * 2 + 4 = 38，38 mod 31 = 7。

还有对多项式进行加、减、乘、除的代码；教科书上一般冗长地称之为加法/减法/乘法/除法。有一个很重要的内容是拉格朗日插值，它将一组x和y坐标作为输入，并返回通过所有这些点的最小多项式（你可以将其视为多项式求值的逆）：

＃构建一个在所有指定x坐标处返回0的多项式

def zpoly(self, xs):

root = [1]

for x in xs:

root.insert(0, 0)

for j in range(len(root)-1):

root[j] -= root[j+1] * x

return [x % self.modulus for x in root]

def lagrange_interp(self, xs, ys):

＃生成主分子多项式，例如(x – x1) * (x – x2) * … * (x – xn)

root = self.zpoly(xs)

＃生成每个值对应的分子多项式，例如，当x = x2时，

＃通过用主分子多项式除以对应的x坐标

# 得到(x – x1) * (x – x3) * … * (x – xn)

nums = [self.div_polys(root, [-x, 1]) for x in xs]

＃通过求出在每个x处的分子多项式来生成分母

denoms = [self.eval_poly_at(nums[i], xs[i]) for i in range(len(xs))]

invdenoms = self.multi_inv(denoms)

＃生成输出多项式，即每个值对应的分子的总和

# 多项式重新调整为具有正确的y值

b = [0 for y in ys]

for i in range(len(xs)):

yslice = self.mul(ys[i], invdenoms[i])

for j in range(len(ys)):

if nums[i][j] and ys[i]:

b[j] += nums[i][j] * yslice

return [x % self.modulus for x in b]

相关数学说明请参阅本文关于“M-of-N”[10]的部分。需要注意的是，我们还有特殊情况方法lagrange_interp_4和lagrange_interp_2来加速次数小于2的拉格朗日插值和次数小于4的多项式运算。

快速傅立叶变换

如果你仔细阅读上述算法，你可能会注意到拉格朗日插值和多点求值（即求在N个点处次数小于N的多项式的值）都需要执行耗费二次时间。举个例子，一千个点的拉格朗日插值需要数百万步才能执行，一百万个点的拉格朗日插值则需要几万亿步。这种超低效率的状况是不可接受的。因此，我们将使用更有效的算法，即快速傅立叶变换。

FFT仅需要O(n * log(n))时间（即1000个点需要约10000步，100万个点需要约2000万步），但它的范围更受限制：其x坐标必须是满足N = 2^k阶的单位根[11]的完整集合。也就是说，如果有N个点，则x坐标必须是某个p的连续幂1，p，p^2，p^3 …，其中，p^N = 1。该算法只需要一个小参数调整就可以令人惊讶地用于多点求值或插值运算。

思考题：

找出模337为1的16次单位根，且该单位根的8次幂模337不为1。

答案是：

59，146，30，297，278，191，307，40

你可以通过进行诸如[print(x) for x in range(337) if pow(x, 16, 337) == 1 and pow(x, 8, 337) != 1]的操作来得到上述答案列表。当然，也有适用于更大模数的更智能的方法：首先，通过查找满足pow(x, 336 // 2, 337) != 1（这些答案很容易找到，其中一个答案是5）的值x来识别单个模337为1的原始根（不是完美的正方形） ，然后取它的(336 / 16)次幂。

以下是算法实现（该实现略微简化，更优化内容请参阅此处的代码[12]）：

def fft(vals, modulus, root_of_unity):

if len(vals) == 1:

return vals

L = fft(vals[::2], modulus, pow(root_of_unity, 2, modulus))

R = fft(vals[1::2], modulus, pow(root_of_unity, 2, modulus))

o = [0 for i in vals]

for i, (x, y) in enumerate(zip(L, R)):

y_times_root = y*pow(root_of_unity, i, modulus)

o[i] = (x+y_times_root) % modulus

o[i+len(L)] = (x-y_times_root) % modulus

return o

def inv_fft(vals, modulus, root_of_unity):

f = PrimeField(modulus)

# Inverse FFT

invlen = f.inv(len(vals))

return [(x*invlen) % modulus for x in

fft(vals, modulus, f.inv(root_of_unity))]

你可以尝试键入几个输入，并检查它是否会在你使用 eval_poly_at时，给出你期望得到的答案。例如：

>>> fft.fft([3,1,4,1,5,9,2,6], 337, 85, inv=True)

[46, 169, 29, 149, 126, 262, 140, 93]

> f = poly_utils.PrimeField(337)

>>> [f.eval_poly_at([46, 169, 29, 149, 126, 262, 140, 93], f.exp(85, i)) for i in range(8)]

[3, 1, 4, 1, 5, 9, 2, 6]

傅立叶变换将[x[0] …. x[n-1]]作为输入，其目标是输出 x[0] + x[1] + … + x[n-1]作为第一个元素， x[0] + x[1] * 2 + … + x[n-1] * w**(n-1) 作为第二个元素等等。快速傅里叶变换通过将数据分成两半，并在这两半数据上进行FFT，然后将结果粘合在一起的方式来实现。

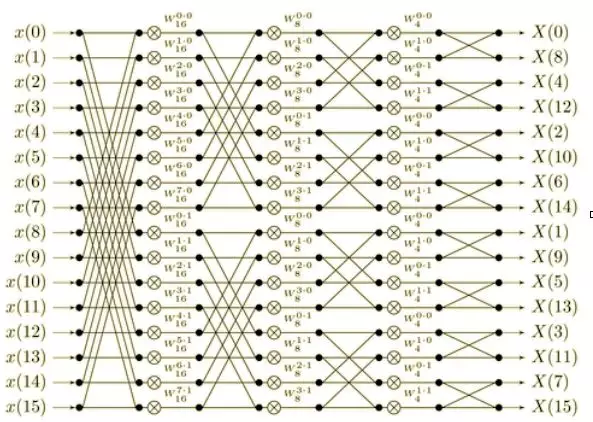
这是信息在FFT计算中的路径图表。注意FFT如何基于数据的两半内容进行两次FFT复制，并进行“粘合”步骤，然后依此类推直到你得到一个元素。

一般而言，想要更直观地了解FFT工作原理以及FFT以及多项式数学，我推荐这篇文章[13]；关于DFT与FFT的一些更具体的细节，我推荐觉得这篇文章[14]的思路还不错。但是请注意，大多数关于傅里叶变换的文献都只谈到关于实数和复数的傅里叶变换，并没有涉及素域。如果你发现这部分内容实在太难了，并且也不想去理解它，那就把它当成某种诡异的巫术就行了——它之所以有用是因为你运行了几次代码并证明这玩意儿确实有用——这样你心里就舒服多了。

本文绝对希望你已经了解模运算和素域的工作原理，并熟悉多项式、插值和求值的概念。否则的话，请回到本系列的第2部分[3]，以及之前关于二次方程式算术的编程的文章[4]。

不存在实现STARK的“唯一正确道路”。它是一种广泛的密码学和数学结构，针对不同应用具有不同的最佳设置。此外，关于减少证明者和验证者复杂度并提高可靠性的研究仍在继续。

考虑到特定应用的效率原因，STARK“在现实生活中”（即在Eli和co的生产实现中实现）倾向于使用二进制域而不是素域。然而，他们确实在他们的着作中强调，基于素域的方法对于本文描述的STARK也是合理并且可行的。

这些代码远非最理想的实现（它们都是用Python编写的，你还想怎么样）

此代码未经过全面审核，生产用例的可靠性无法保证