在上一篇 ZKSwap团队解读零知识证明PLONK电路 主要描述了PLONK协议里的一个核心部分,用置换校验的方法去证明电路门之间的一致性;接下来,将继续分享如何证明门的约束关系的成立,以及整体的协议剖析。
门约束
举个简单的例子,假如存在一个电路,电路中仅有3个乘法门,对应的约束如下:
L1 * R1 – O1 = 0
L2 * R2 – O2 = 0
L3 * R3 – O3 = 0
进行多项式压缩:定义多项式函数L(X)、R(X)、O(X) 满足:
L(1) = L1, R(1) = R1, O(1) = O1
L(2) = L2, R(2) = R2, O(2) = O2
L(3) = L3, R(3) = R3, O(3) = O3
此时,定义新的多项式函数F(X),令F(X) = L(X) * R(X) – O(X)
则有:
F(1) = L(1) * R(1) – O(1) = 0
F(2) = L(2) * R(2) – O(2) = 0
F(3) = L(3) * R(3) – O(3) = 0
也就是表明:如果多项式函数F(X)在X=1、2、3处有零点,则说明门关系约束成立。
多项式函数F(X)在X=1、2、3处有零点则表明多项式F(X)可以被(X – 1)(X – 2)(X – 3)整除,为了和论文一致,我们把这个多项式函数设置成Z(X),即:
F(X) = T(X) * Z(X) ==> T(X) = F(X) / Z(X)
如果能证明T(X)是一个多项式,则说明多项式F(X)与Z(X)有相同的零点,进而说明门约束关系成立。
一般过程应该如下:
- P计算F(X)并把F(X)发送给V;
- V根据Z(X)直接校验F(X) / Z(X)
但是如此过程存在两个问题,一个是复杂性问题,假如F(X)的阶为n,那通信复杂度就是O(n);而是安全性问题,多项式F(X)完全暴露给V。
那应该如何解决这两个问题呢?最佳的答案可能就是:多项式承诺
多项式承诺
什么是多项式承诺?就是证明方P用一个很短的数据来代表一个多项式F,这些很短的数据可以被验证方V用来验证多项式F在某一点的值确实为证明方P声称的值z。
具体看一下论文里的定义:

由图可知:
- Setup:初始化,生成计算多项式承诺需要的一些必备参数;
- Commit:计算多项式承诺,其结果是一个值;
- Open:返回与多项式承诺对应的多项式函数;
- VerifyPoly:验证多项式承诺是否和多项式函数一致;
- CreateWitness:证明多项式函数在某一点的值是否是证明方P声称的值,具体的数学方法就是:判断多项式是否能被整除,即:
- VerifyEval:验证方V验证多项式函数在某一点的值是否是证明方P声称的值,具体的数学方法是:利用双线性配对验证其数学乘法逻辑关系。
继续回到我们上面的问题:
证明方如何证明:T(X) = F(X) / Z(X),我们再简化一下场景,就令Z(X) = X – 1,则:
T(X) = F(X) / (X – 1) ==> T(X) * (X – 1) = F(X) ==> T(X) * X = F(X) + T(X)
对应多项式承诺的协议可知:证明方P其实是想证明多项式函数F(X)再X = 1处的值为0,因此根据协验证方只需要证明:
e(Commit(T(x)), x*G) =? e(Commit(F(x)) +Commit (T(x)), G) (双线性配对的性质)
可以看出,利用多项式承诺的数学工具,既可以实现复杂度的优化,又可以实现隐私保护。
协议
接下来分析一下完整的PLONK协议:
Relation
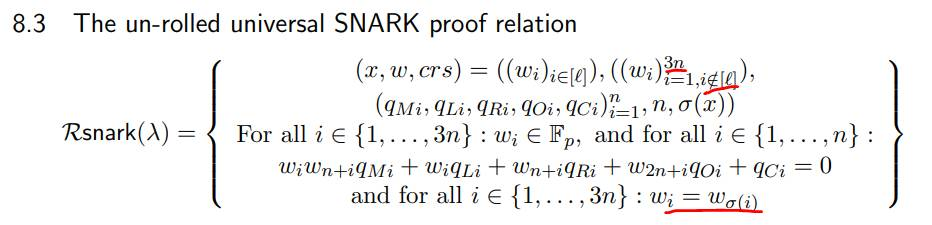
上图表示了PLONK算法里,要证明的一种关系,需要说明的是:
- w 代表着电路里的输入、输出,总共3n个,n是电路里乘法门的数量,每个门都有左输入,右输入和输出,因此w总共有3n个;
- q* 代表着选择向量,它的取值对应这这个是乘法门,还是加法门等类似的约束类型
- σ 代表着置换多项式,其表示门之间的一致性约束索引
- 倒数第一个公式代表 门之间的约束成立
- 倒数第二个公式代表 门的约束关系成立
CRS & P_Input & V_Input
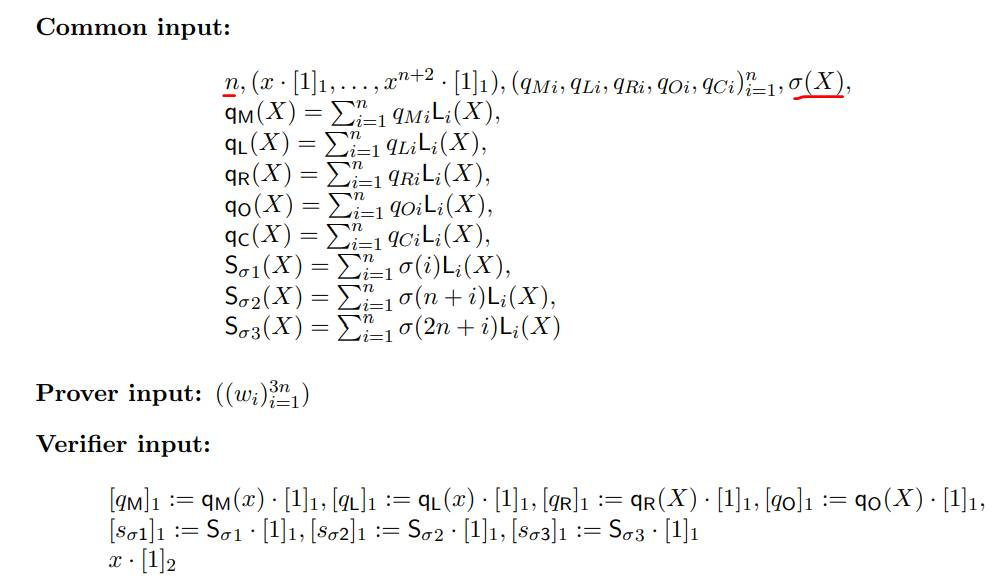
上图表示了PLONK算法里的CRS设置,以及证明方P和验证方V的一些输入,需要说明的是:
- 整个协议都是基于多项式的,因此需要构建对应的多项式形式。
- 多项式σ的阶是3n的,由于和多项式承诺相关的CRS最高的阶位n+2,因此需要把σ拆分成3个多项式S,分别记录每个多项式的置换关系(L、R、O);
- 为了减少通信复杂度和保护隐私,协议基于多项式承诺构建,因此验证方V的输入都是承诺值。
Prove
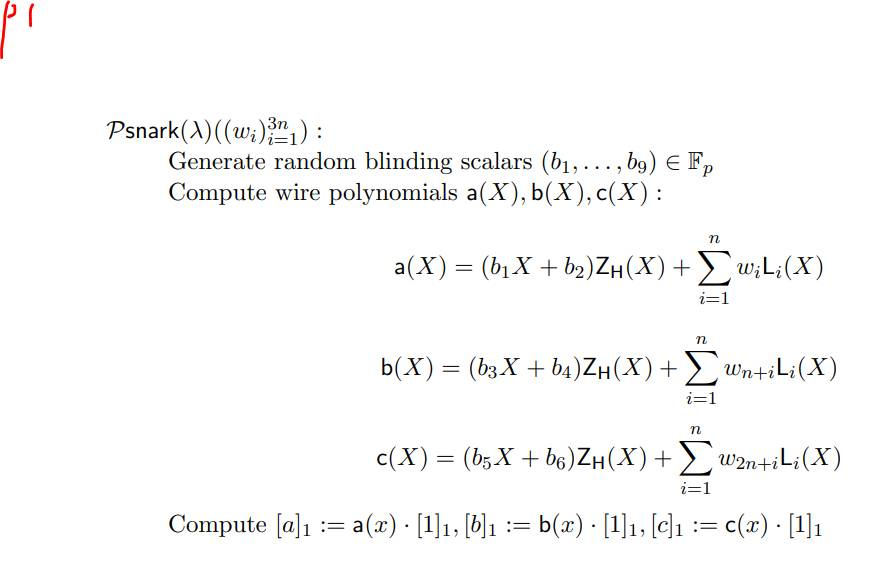
上图表示了PLONK算法里证明方的一些操作,需要说明的是:
- b1…b9是随机数,从用法看是为了安全,但是我暂时也没明白,不加这个随机数,又会有什么安全问题?
- a(X)、b(X)、c(X)分别是代表了电路里的左输入,右输入和输出
- [a]、[b]、[c]表示多项式的承诺值,参考多项式承诺小节里的承诺计算方法

上图表示了PLONK算法里证明方的一些操作,主要是置换校验,参考第一篇的置换校验的协议过程,生成多项式z(X),需要说明的是:
- β和ϒ都是用来生成置换校验函数的参数,详见第一篇里f(x)和g(x)的生成过程;
- z(X)的生成方式对应置换校验里跨多项式的生成过程,Li(X)为拉格朗日多项式基,性质满足,尽在x=i的时候为1,其他为0;
- 注意区分ω和w,ω是群H的生成元,是多项式的自变量的取值。w是电路的左输入,右输入和输出,是多项式L,R,O在在群H上的取值。

上图表示了PLONK算法里证明方P的一些操作,主要是把门约束和门之间的一致性约束组合到一起,通过α,需要说明的是:
- 根据前面的描述,门约束多项式和一致性约束多项式在群H上的所有元素都是取值为0的,因此都会被多项式ZH(X)整除,等同于上面所述的T(X);
- 因此,证明方只要能证明整除的结果的确是多项式,那就能证明,门约束多项式和一致性多项式在群H所有元素上取值为0,即所有约束关系成立,即电路逻辑成立;
- 可以知道的是t(X)的阶最高为3n,但是用于计算承诺的CRS只到了n的级别,因此需要把多项式t(X)拆分,然后单独计算承诺值。

上图表示了PLONK算法了证明方P的一些操作,主要根据多项式承诺的协议,前面P算出了多个多项式在点x=z处的值是多少,现在要用多项式承诺协议去证明,这些计算是正确的,需要说明的是:
- 为了减少验证方V的操作复杂度,t(X)的分子部分r(X)在x=z处的值,P计算好,然后验证方直接验证,其他的操作类似;
- v的值看起来是为了更安全;
- Wz(X)对应多项式协议里的CreateWitness操作,证明这些多项式r(X),a(X),b(X)等在x=z处的值确实等于r,a,b等,对Wzw(X)同理,并返回承诺值。
Verify
至此,证明方P的所有操作都完事了,接下来都是验证方V的操作。
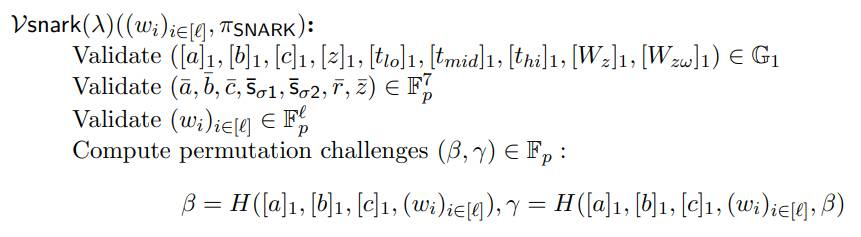
上图表示了PLONK算法里验证方V的一些操作,主要重新生成相关的参数,确保证明方P没有作恶。需要说明的是:
- 从输入看,比较清晰,就是一些公开的输入和证明方P的证明输出;
- 根据输入,生成置换校验过程中需要的一些参数

上图表示了PLONK算法里验证方V的一些操作,对于一些公开的,并且计算复杂度很小的多项式,其在x=z处的值还是需要自己计算,更为方便。需要说明的是:
- 根据证明方P的过程来看,验证方V的核心工作就是验证两个多项式承诺;
- 两个多项式承诺验证需要两个配对,可以通过一个参数组合成一个配对,即μ;
- 在验证前,先计算Wz(x),Wzw(x)的分母在x=z处的值,两部分,减数和被减数,分别对应[F]、[E]。μ作为系数的,就是对应Wzw(X)多项式的。
- 最后通过一个双线性配对操作完成两个多项式承诺的验证。
结束
至此,PLONK算法的协议原理已全部分享完成,公式很密集,但是细分下来,又很有层次感。能坚持看完,已实属不易。
原创文章,作者:CoinKaola,如若转载,请注明出处:https://www.coinkaola.co/news/209229/






