科普 | Casper FFG 的可审计安全性和近似活性


作者: Aditya Asgaonkar
翻译&校对: IAN LIU & 阿剑
来源:以太坊爱好者
感谢 Carl Beekhuizen 的审阅。
区块链需要向用户提供两种保障—— 1)区块的确定性(finality)和 2).区块链的活性(liveness)—— 区块链的底层共识机制就负责提供这两种保障。以太坊 2.0 中 ,共识过程只在信标链(beacon chain)上发生,并使用 Casper Friendly Finality Gadget (FFG) 机制来帮助达成共识。本篇文章旨在描述基本的 FFG 机制,并证明它能提供上述两种保障。
Casper FFG 是一种“确定性工具”,这意味着 Casper FFG 规范了区块的确定性规则,并能在事件发生之后检查区块的确定性。FFG 机制与链的增长脱钩,可以作为独立组件附加在任意可用的区块链协议上来提供区块确定性。因为 Casper FFG 机制没有能够保证区块链活性的策略,因此从这个角度来看,它并不算是完全成熟的共识协议。(也许之后我会再写一篇 关于以太坊 2.0 信标链的活性注意事项 的文章!) 让我们先从 Casper FFG 的结构开始,然后深入 Casper FFG 机制的规则,最终了解它提供的安全性 & 活性保证。
投票
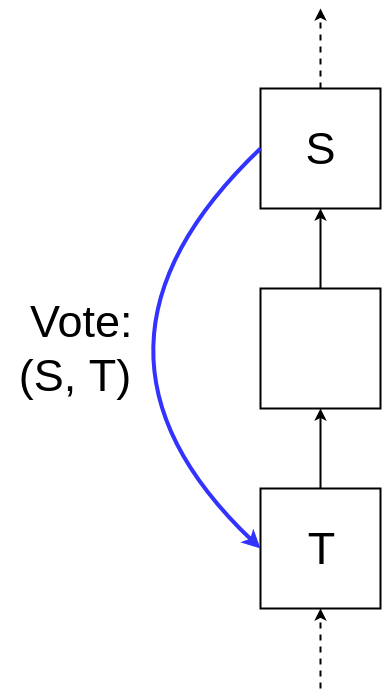
验证者通过提交见证消息(表明自己认为的 “有效转换(valid transitions)”)来对链上的区块投票。投票的格式为(S, T),包含两部分信息:来源区块(S)目标区块(T)—— 目标区块必须是 S 的派生区块具体来说,投票所包含的信息包括验证者的数字签名、用于确认区块的区块哈希和块高。
合理化(Justification)与确定性达成(Finalization)
合理化(Justification)与确定性达成(Finalization)是 Casper FFG 共识过程的两个阶段,可以和传统拜占庭容错(BFT)共识的 “prepare” 和 “commit” 阶段做横向对比。
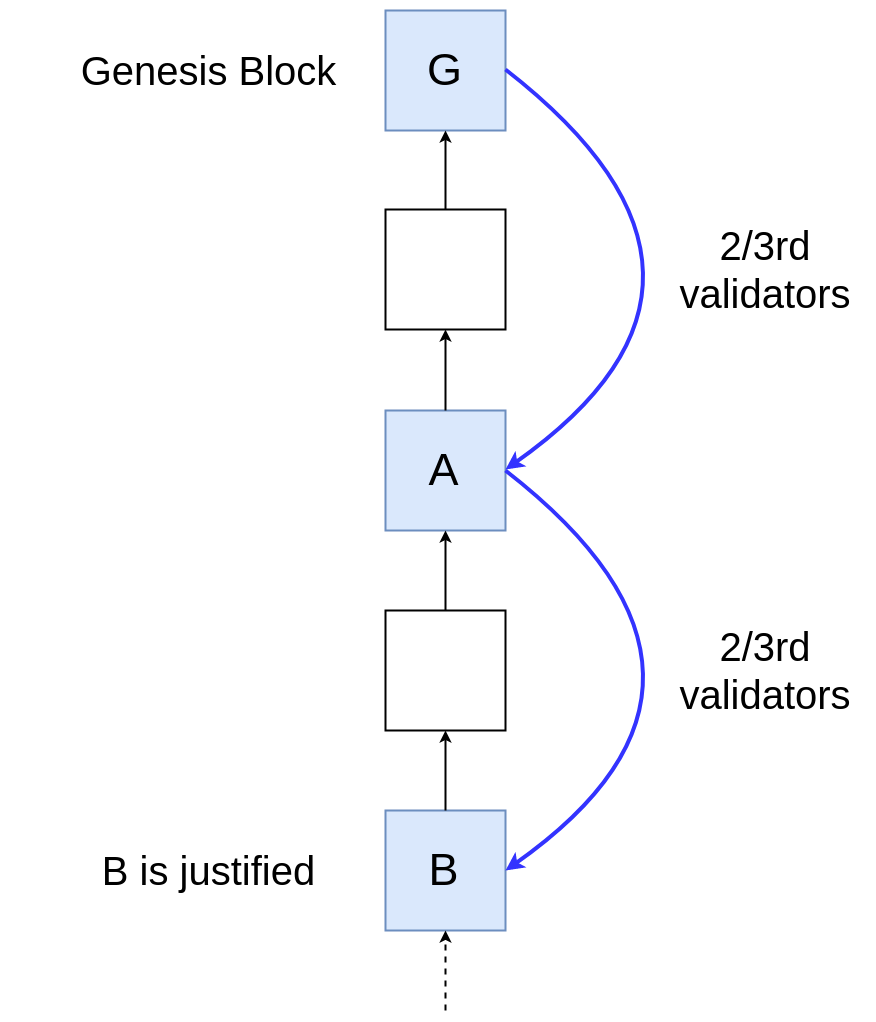
- 因具备 2/3 以上的验证者投票,区块 A & 区块 B 得到合理化 -
合理化 :只要某区块 B 满足下列条件,则该块就被合理化:
-
区块 B 是创世区块,或 -
超过 2/3 以上的验证者将选票投给 (A, B),其中 B 是 A 的后代区块,且 A 在此前已被合理化。
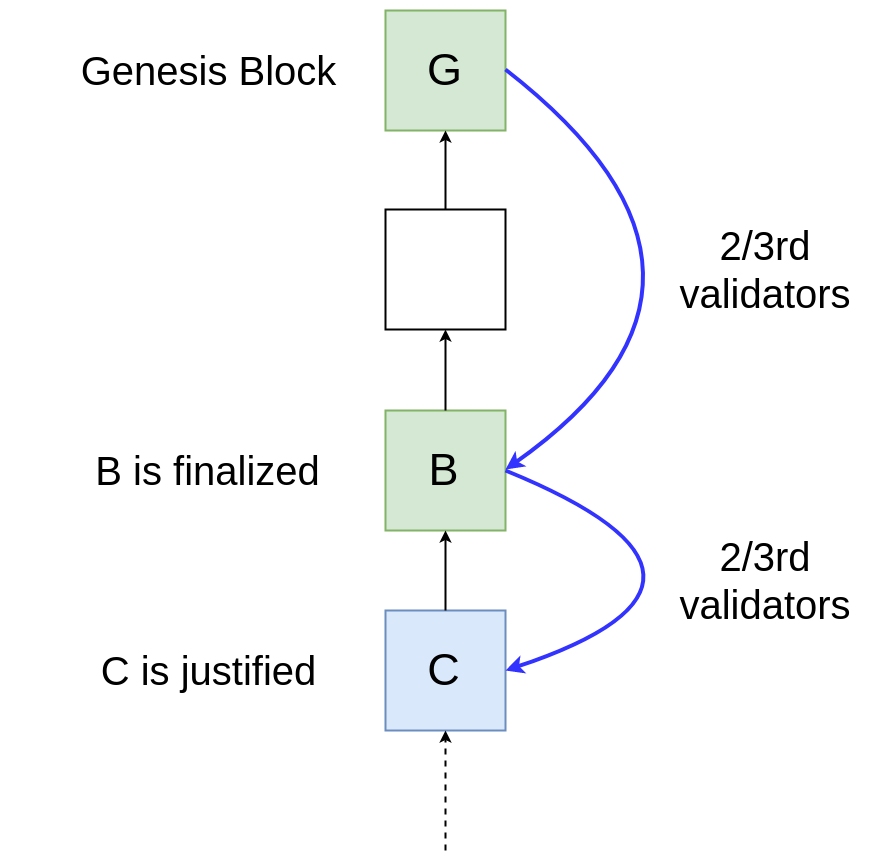
确定性 :只要区块 B 满足以下条件,即获得确定性:
-
区块 B 是创世区块,或 -
B 已满足合理性,且有超过 2/3 的验证者选票投给 (B, C),其中 C 是 B 的直系子块(即,区块高度(C) = 区块高度(B) + 1 )。
Casper FFG 规则
Casper FFG 只有两条简单的限制规则,应用这两个规则就能防止验证者同时给 (S1, T1) 和 (S2, T2) 投票:
(Casper FFG 不允许:)
-
区块高度(T1) = 区块高度(T2),或 -
区块高度(S1) < 区块高度(S2) < 区块高度(T2) < 区块高度(T1)
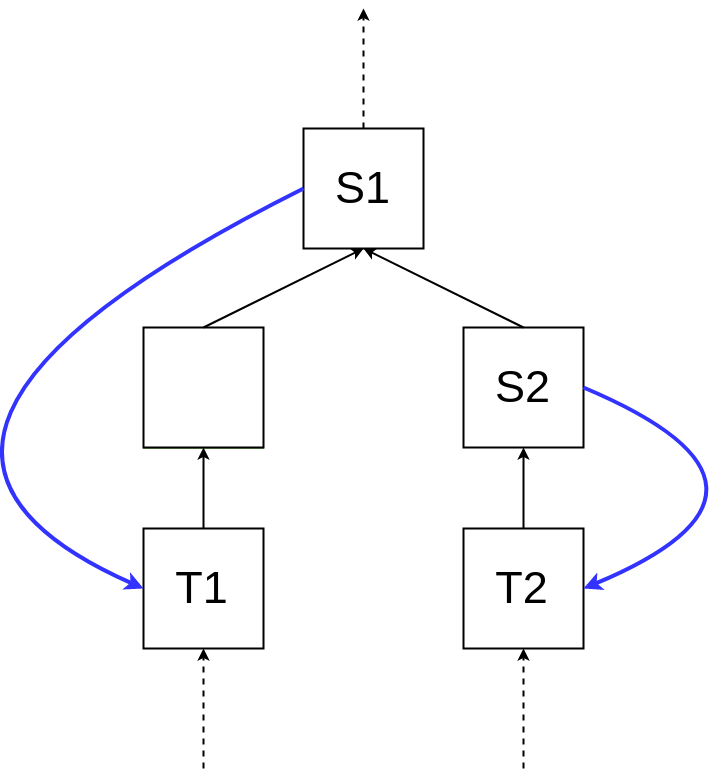
- Casper FFG 规则违反情况一 :区块高度(T1) = 区块高度(T2) (译者注:即所谓的 “双重投票”)-
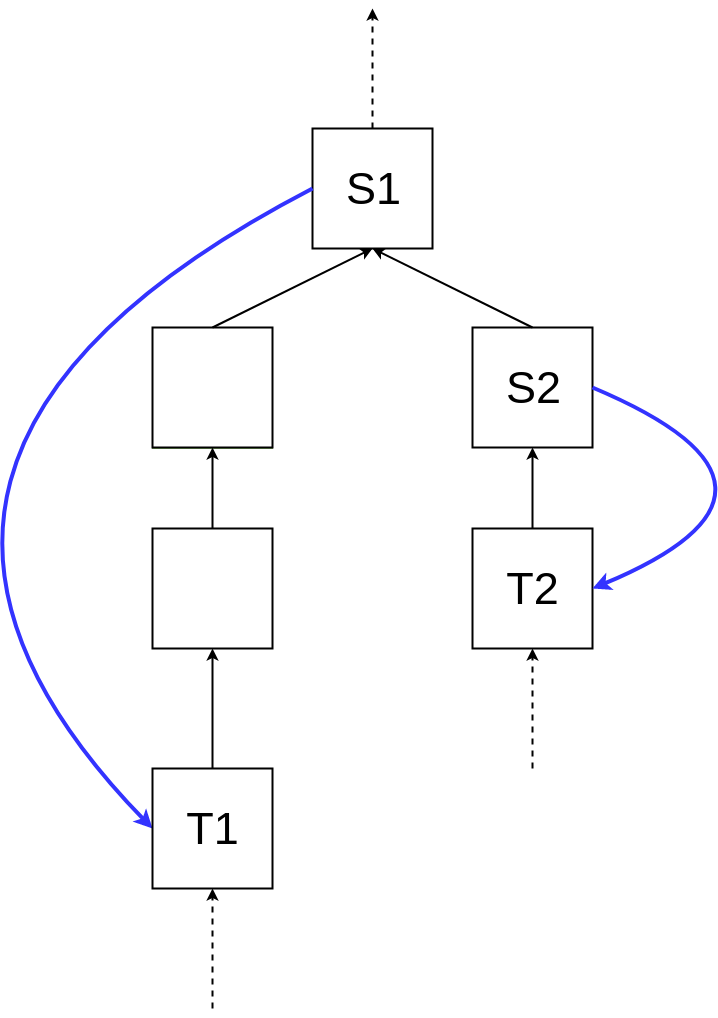
- Casper FFG 规则违反情况二 :区块高度(S1) < 区块高度(S2) < 区块高度(T2) < 区块高度(T1) (译者注:即所谓的 “环绕投票”)-
安全性 & 活性
-
可追责的安全性 :如果两个相互冲突的区块都达成了确定性,则至少有 1/3 的验证者违反 Casper FFG 规则,而 Casper FFG 可以识别出这些验证者。 -
近似活性 :无论协议运行处于什么状态,验证者都能继续履行职责、能在不违反 Casper FFG 规则的前提下敲定新区块。
事实上,熟悉 BFT 文献的人可能会觉得 “ 近似活性 ” 的概念简直异想天开;不过因为 Casper FFG 只是“确定性工具”,整个机制只要确保诚实的验证者能在不违反 FFG 规则的情况下推动推进协议,而不会被卡在任何一个环节,即可。
至于可追责安全性的定义,我们的重点是可追责性(即能够识别出违反规则的验证者),然后这部分信息能够被权益证明机制沿用、用于在区块链上处罚恶意验证者。最终目的还是为权益证明机制提供信息,使后者的激励机制能生效,促使共识过程形成协议一开始设想的均衡状态。
安全性证明
-
区块高度(A) = 区块高度(B) -
因为 A 和 B 在得到确定性之前先要获得合理性,则它们 各自 都要收到至少 2/3 的验证者投票,这意味着一旦它俩都达到要求,则至少有 1/3 的验证者违反了 Casper FFG 规则。
-
-
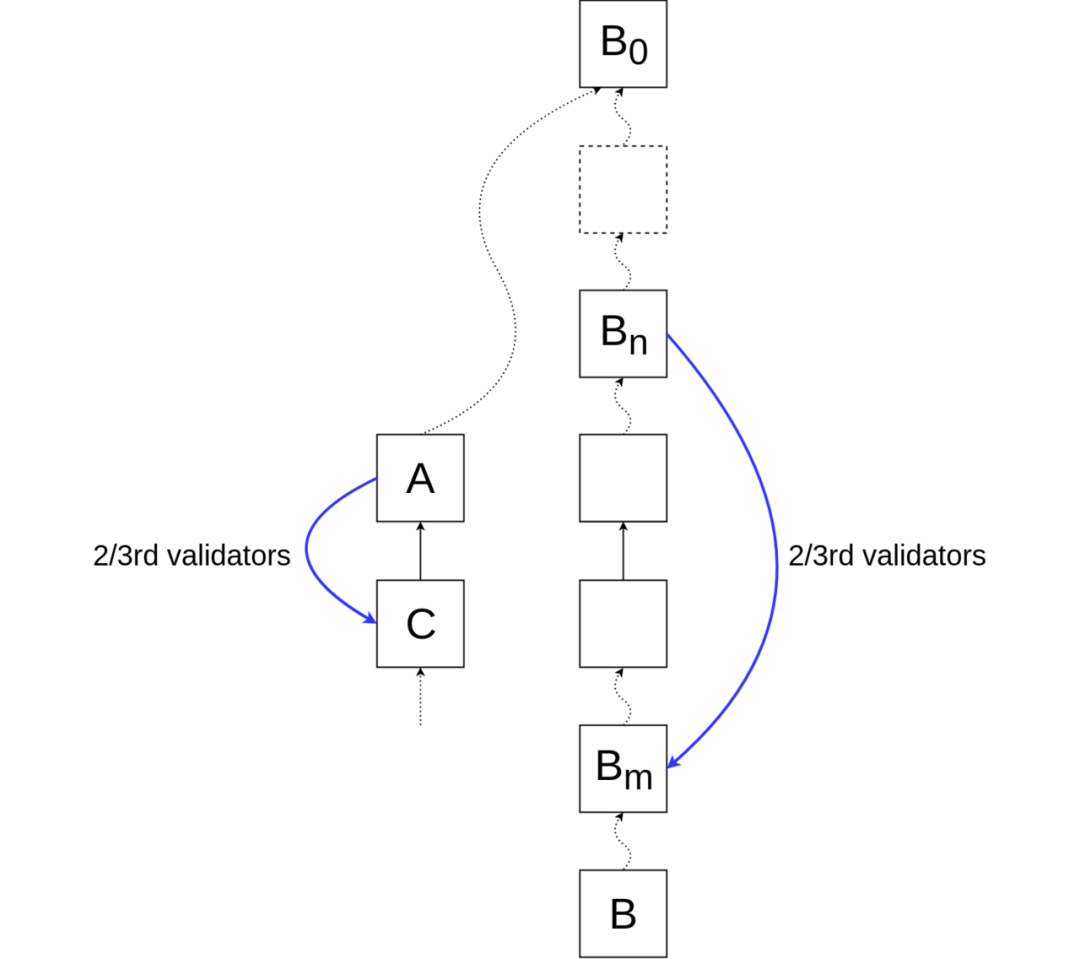
区块高度(A) < 区块高度(B) (具备普适性) -
为了让 A 达成确定性,需要超过 2/3 以上的验证者将选票投给 (A, C),其中 C 是 A 的子块。 -
为了让 B 达成合理性,则在 B 之前必须存在连续升序的区块(创世块、B_0、 B_1、 ... 、B_n、B),且每个区块都已经被它的后一区块合理化(即,至少 2/3 的验证者投票给(G, B_0)、(B_0, B_1)、...... )。假设区块 B_m 是这串连续区块中的首块,区块高度(A) < 区块高度(B_m)。 -
注意,这串连续的区块不存在与区块 A 或 C 相同的块高,不然就变成了上一种情形(块高相等的冲突区块情形,违反 Casper FFG 规则一) 。 -
现在假设我们将票投给 (B_n, B_m) (其中 n = m-1) ,使得 B_m 获得合理性。则因为区块高度(B_m)、区块高度(B_m) 皆 不等于 区块高度(A) /区块高度(C),因此情况一定是区块高度(B_n) < 区块高度(A) < 区块高度(C) < 区块高度(B_m)。 -
这样一来我们就能说——至少有 2/3 的验证者违反了 Casper FFG 规则二。
-
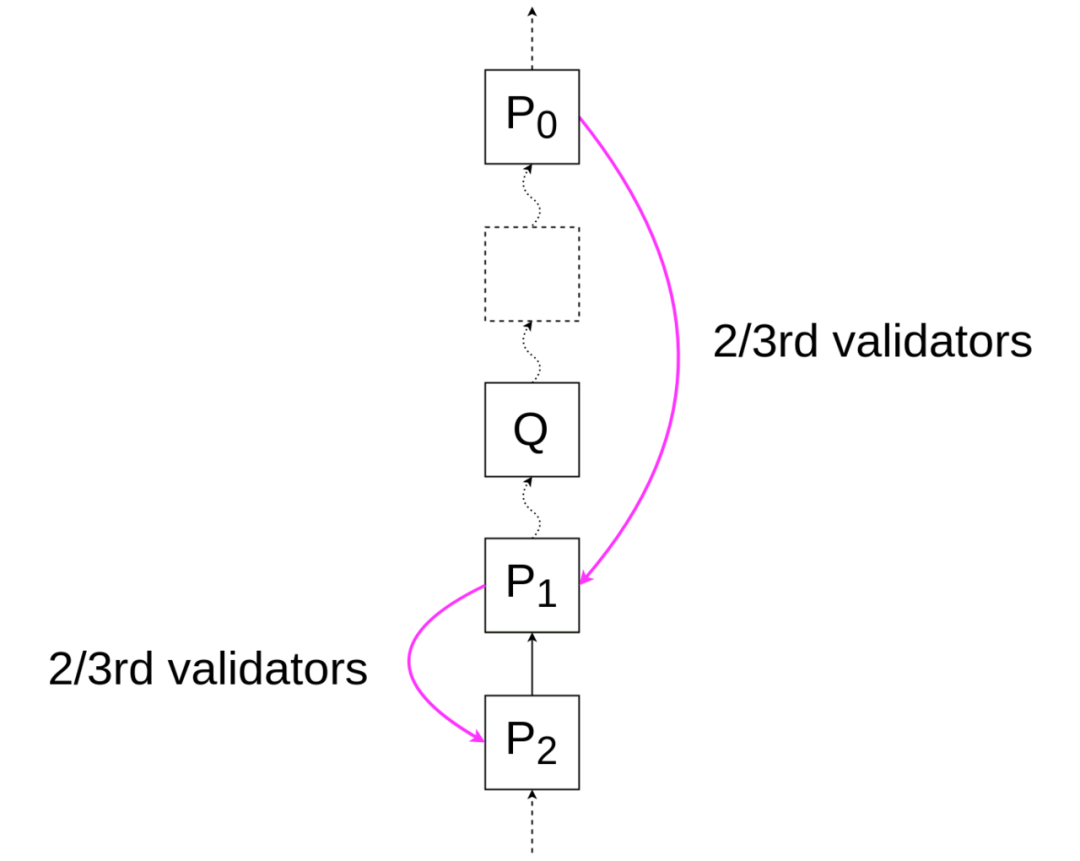
活性证明
-
假设 P_0 是最新的合理区块,Q 是曾得到过验证者投票的最新区块。 -
接下来,任何属于 P_0 子块的区块 P_1(区块高度(Q) < 区块高度(P_1) )都能在不违反 FFG 规则的情况下收到 2/3 验证者的的投票(P_0, P_1),进而取得合理性。 -
P_1 也能在不违反 FFG 规则的情况下收到 2/3 验证者的的投票 (P_1, P_2),进而获得确定性,其中 P_2 是 P_1 的子块。
进阶阅读材料
-
Casper FFG 初版论文 —— Casper the Friendly Finality Gadget -
对 Eth2.0 应用 Casper FFG 方法的分析 —— Combining GHOST and Casper